With all the talk about turbulence in Part 3, I am hoping that I didn’t leave with the impression that our galaxy has been left simply chaotic, random, and just a mess as a result. Nothing could be further from the truth. We should not at all despair about chaotic (or more precisely – non linearly dynamic) systems such as a galaxy- a lot of order comes from chaos – patterns emerge that are both complex and beautiful. Indeed, all galaxies are going to be unique and to be honest, this is a good thing or our hobby of imaging them would get tired very quickly. Dealing with dynamic systems such as a galaxy is very different from trying to understand a static one. The main difference is that in a dynamic system, the components are moving relative to other components requiring different frames of reference to be taken in order to understand them and ensure that both static and dynamic forces are all in balance.
Unlike any astrophysical or cosmological explanations I have seen or read, the explanation that is posited introduces a new force not considered by conventional astrophysics / cosmology and a more realistic, if a bit more complex, representation of the thermodynamics of hydrogen at play. The new force, is actually viscous forces or more commonly described in astronomy as friction. Neither fluid mechanics nor thermodynamics is new to “earthbound” scientists however, it is somewhat alien to the astronomy world, just as “dark matter” is to we scientists on the ground. In Parts 1 and 2 of this series of posting, I have shown why the overall shape and structure of the galaxy is oblate and takes the form of a torus or a donut. In Part 3, I introduced viscous forces and fluid mechanics and showed how the galactic orbiting hydrogen is in a state of turbulence resulting in the hydrogen separating into two states, atomic hydrogen ISM occupying most of the space in our torus, and molecular cloud (MC) hydrogen, comprising most of the mass. The MCs that are created are what will become the spiral arms of our galaxy and the viscous forces and phase separation are what give them materiality. Most astrophysicists and cosmologists, in defense of their “ideal gas” assumption for hydrogen, would argue that the spiral arms cannot be material due to something called “the winding problem”.
Ultimately any solution to the winding problem first requires a description of what the spiral arms physically are and why they exist. Most current theories suggest that the spiral arms are merely regions of higher ISM (monatomic hydrogen) pressure caused by the interference of galactic material in two phases. We are all aware that both the ISM and the stars are two phases of hydrogen, so naturally astronomers have turned to the interaction of these two phases as the source for the galactic arms. But there are all kinds of arguments why this must be wrong – most of them stemming from the extremely stalwart assumption of “ideal gas behavior” of hydrogen when it is in its non-starry, or gaseous, form (ie. devoid of fluid mechanical or thermodynamic reality). I will list but a few here, as I could go on and on and on.
- We know molecular clouds exist and that is where stars are created and these clouds tend to be in what we call the spiral arms. How can an ideal gas behave as two different things at once?
- There is a huge chicken/egg problem with using stars as cause for the spiral arms. Aren’t arms required to make stars, while stars are required to make the arms? JWST has recently shown that spiral galaxies appear in the universe much earlier than anticipated if we had to wait for stars to form first.
- There is missing mass when we count up all the monatomic hydrogen and starry hydrogen, resulting in the need for a “dark matter” correction.
In this current, Part 4 posting, I will show how the two phases that naturally result from the inclusion of both the fluid mechanical and thermodynamics properties of hydrogen, create our spiral forms. I will be describing the mechanical properties of this two phase system (MC and ISM) and why the forces acting on them make them behave the way they do, and can be material while still avoiding the “winding problem” at the same time. There will be no need for stars in this stable structure, and how the structure can recover from perturbations. In Part 5, I will show how the “peculiar” star velocity profile used to justify dark matter actually falls directly from treating the spiral arms as material (another thermodynamic phase), and why diatomic hydrogen is the likely source of the missing mass.
After describing the properties of our MC spiral arms I will be employing the “free body diagram” mechanical engineering method of analysis. This involves determining the various forces as vectors having direction and magnitude and acting on a body. If all of the forces balance out and cancel each other out, there will be no acceleration of the body in space. The process also looks at where on the body, different forces act, because any unresolved bending moments will cause a change in rotation or shape of the body itself. This approach is will lead to an explanation and description of the overall gravitational field associated with a spiral galaxy – at least as far as its gaseous hydrogen. I will be doing most of this analysis in a frame of reference that is rotating with the same time period as the galaxy. This allows us to treat angular momentum as a centrifugal force that acts to pull material away from its centre of gravity, just as gravity itself pulls material towards it. Once we balance gravity and centrifugal force everywhere on the spiral arms, we can satisfy ourselves that they will not move relative to one another and the whole thing can orbit the galactic centre.
To get you thinking about orbits and frames of reference, I would like to tell a short tale of a naturalist who happens to glance a squirrel running up a tree trunk, perhaps startled by the movement of the naturalist. The squirrel runs up the trunk opposite the naturalist so that he is hidden from the naturalist. The naturalist wants to take a look at the squirrel so she starts to move around the tree to get a better look. The naturalist also , as she moves around the tree, will also move further away from the tree, in order to increase her view of both sides of the tree trunk. Or perhaps she moves closer to the tree to get a better look at squirrel and increase here chances of catching up to it. The squirrel can see the shadow movements of the naturalist and also moves around the tree, staying on the opposite side at all times – hiding from the naturalist. From the naturalists point of view, she eventually ends up walking completely around the tree back to her starting position, once her orbital distance has stabilizied between her need to catch up to the squirrel with her need to see around the tree. All without ever actually seeing the squirrel.
To an outside observer watching this dance, it may appear that she has been orbiting the tree, whereas she has been orbiting the squirrel and the squirrel has been orbiting the tree. The naturalist is really attracted to the squirrel, and not the tree (she has seen plenty of trees before), but as she tries to orbit the squirrel, she finds herself orbiting the tree as well. The squirrel knows enough that it is smaller than the diameter of the tree, so if it keeps its period (orbital time around the tree) the same as the naturalist, it will never be seen. If we take a frame of reference of turning around the tree at the same period as the naturalist/squirrel turns, the relative position of the squirrel and the naturalist will not change. The view will never be reached by the naturalist, as she will only get a view of where the squirrel will be or was – half a period ago or in the future. In this rotating frame of reference, the relative position of the squirrel and the naturalist does not change. We will be using this rotating frame of reference in our galactic description.
One last twist to our story, before moving on. The squirrel in the story need not exist, perhaps it runs up the tree and gets away. The only thing critical to the naturalist’s movement is her belief that the squirrel is there, on the other side of the tree. As long as she is determined to see the squirrel and believes it is there she will continue to orbit the tree. In this posting, we will be solving a problem that involves a rotating frame of reference, only the role of the tree will be played by a central black hole in the galaxy, the role of naturalist will be played by the a segment of the galactic spiral arm, and the squirrel will be played by a virtual centre of gravity of the spiral arm. Now I say “virtual” centre of gravity, because there is nothing actually there – no squirrel, but the superposition of two gravitational fields makes the galactic spiral arms “believe” it is there and therefore – rotates around it. This virtual centre of gravity also rotates around the black hole in the centre of the galaxy at the same period as the galactic arm and their positions are static or unchanging in our rotating frame of reference.
Back to the title of this posting – the solution to the “Winding Problem”, or “why don’t the spiral arms wind upon themselves as they revolve around the central attractor or black hole at the centre of the galaxy (ie. our fabled “tree”)?”. The winding problem arises because under the gravity of a central attractor or even a disk of matter, the arms of the galaxy move faster, but at a longer period than the arms closer to the black hole. Since the orbital period is not constant over all radii, the arms wind upon themselves and this winding continues until we end up with a mass with no arms at all. This is the equivalent of our squirrel moving faster than the naturalist, and in our rotating frame of reference the naturalist and squirrel will moving relative to each other and the squirrel’s cover will be blown.
Solving the winding problem involves coming up with a scenerio – supported by the viscous forces at play, that all spiral arms orbit the galaxy at a constant period (or tau). This is not easy, because the spiral arms at greater radius from the centre, have to travel a greater distance to get around the galaxy in the same time period. This means that the centrifugal forces has to get greater the further away from the centre that the galactic arm is. In turn, this means that the gravitational force on the spiral arms must get greater the further away from the centre in order for the two opposing forces to balance. We know that gravity tends to get weaker (smaller acceleration to the centre) rather than stronger with distance (actually with radius squared) – whether we model the galactic pull of a black hole, a single phase disc of material, or a combination of the two. This means that no matter how we model the hydrogen material as a single phase, we end up with the spiral arms taking longer to orbit the galaxy the further out they are, and the “winding problem” results.
Animation1: The animation demonstrates the winding problem that will occur if the period of rotation of the spiral arms is allowed vary with the radius of rotation. The spiral would draw particles inward toward the centre as they wrapped around each other until forming a tighter higher pressure mass around the centre. With each wrap or wind, the shearing between windings would increase as the winds getting closer together. For a disk shape to avoid the winding problem, gravity must counter centrifugal force at all radii, but this condition cannot be achieved.
Note that the winding problem is essentially the opposite of cavitation.
Credit Wikipedia
This winding issue, with the arms getting wrapped tighter and tighter upon each other isn’t observed either directly (through visible Ha spectral emissions) or indirectly via stars and dust. In fact, the ever-tightening winding must ultimately result in the homogenization of the arms into continuous disc after a only few revolutions. This winding is in essence, the opposite of the cavitation we described in Part 3 of this post series, that describes the “delamination” and expansion of the galaxy. But we will go much farther than this here.
Animation 2: This animation is meant to show where the stars are, and as a result it is a little blurry, but the animation is still useful but I want you to think of the spiral arms instead of stars. In this animation, the spiral arms act as if they were solid, moving with a constant period of rotation, or “tau” regardless of their radial distance from the centre. Since the arms of the galaxy gaseous, and not solid this means that the forces acting on the spiral arms must always in balance. Furthermore, small perturbations causing any imbalance must result in a return to balance for the galaxy to remain stable. Note that on the wikipedia site, this animation is labelled as “wrong”, and in fact the website is correct in that it is indeed wrong for the orbit of stars (that will be discussed in the ultimate (Part 5) of this post series when I add stars and dust to the galaxy. The animation is actually correct for our still invisible spiral MC arms/ropes, even though they are not rigid bodies. Nonetheless, this animation is known as a “rigid body” rotation with constant “tau”. Credit Wikipedia
The crux of the winding problem is that the spiral arms of the galaxy need to have the same orbital period, tau (wordpress doesn’t do greek letters), regardless of the spiral arm position. That way the galactic arms will move in sync, just as our squirrel moves in sync with the naturalist.
If you happen to remain a doubter of the materiality of the spiral discs, I would first like to tackle the issue with this approach – as if there is no materiality to them to see how far it gets us. As it turns out there is a condition that exists whereby and single phase disc of material could orbit a central point with a constant orbital period, or tau, (or synchronicity – same time), and that is by somehow distributing material such that the acceleration of gravity to be a function of radius that would equal the same functionality of centrifugal force with radius. As it turns out, tau would be constant if the gravitational acceleration were a linear function of radius, directly mimicking the linear dependence of centrifugal force on radius under a constant tau.
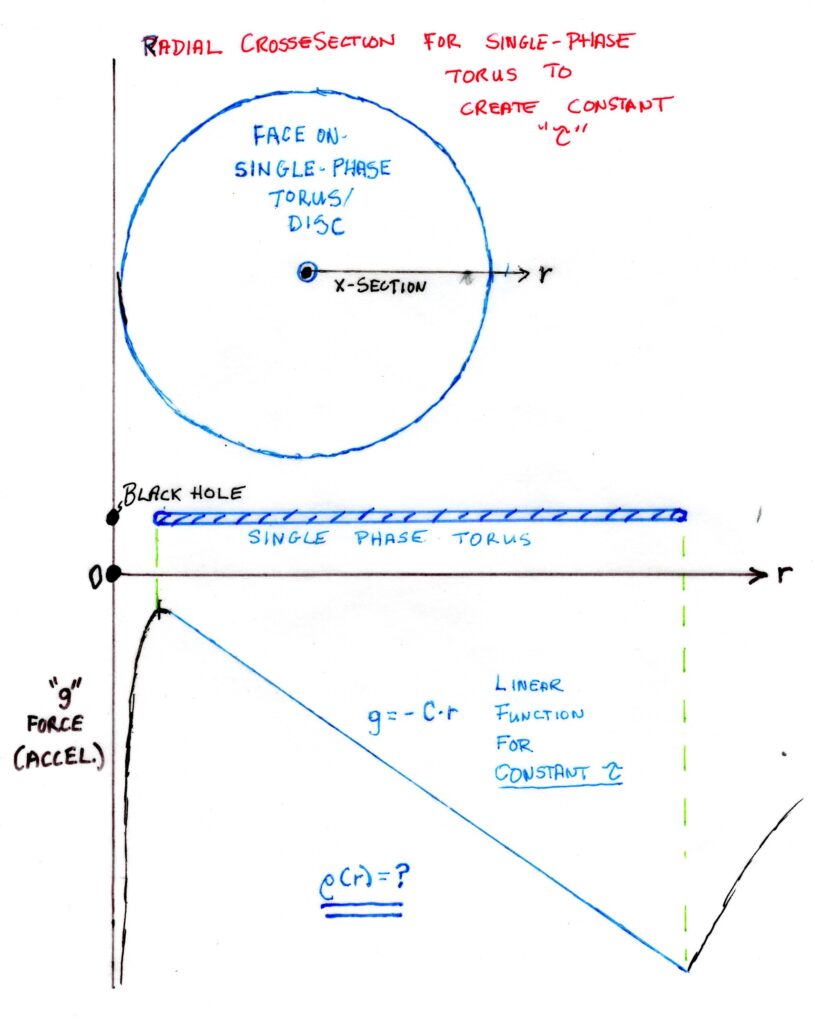
A graph of the hypothetical radial gravitational force on our toroidal galactic disk is shown here, with the sign convention of being a negative radial g-force representing acceleration when it is toward the galactic centre. Near the centre, the inward pull of gravity is dominated by the central black hole and the g-force is highly negative (just as one would expect around a black hole). However, as we move radially away from the centre of our toroidal galaxy, the outward pull of the torus mass causing the g-force to rise (become less negative) than it would have with the black-hole alone. The g-force actually peaks as the inner radius of the toroidal disk is reached. The peak g-force must remain negative or it is an indication that the central attractor is not massive enough relative to the mass and angular momentum to hold the galaxy. As we then continue to move outward through the actual torus itself in our hypothetical gravitational curve, the gravitational force must decreases again (becomes a larger negative) – more and more of the toroidal hydrogen mass lies inward compared to the amount of mass outward. This makes the the gravity more negative with radial distance. In order to maintain synchronicity as in our second animation, the g force must get stronger with radius in a linear (straight line) manner. If this can be achieved, then both gravity and centrifugal forces can match everywhere, as well as both vary linearly with distance from the centre, and the whole thing can move with a constant period.
Mathematically, we have shown that the winding problem can be solved if the orbital period, tau, can be made constant throughout the torus. Such a condition can only occur in a single phase if the g force is an linear function of radius, ie. g=-C*r, where C is a constant), as shown in the graph. At this point astrophysicists and cosmologists hit a brick wall. While the g-force within the torus is dependent on the radial density distribution of the hydrogen, there is no physical continuous single phase distribution that can result in this linear function of g-force with radius – ie. it is unphysical. In other words, the winding problem is unsolvable as long as we state that there is only one phase of hydrogen in the disc. As a result, the winding problem continues to be a major puzzle to the astronomy community, as long as we continue to believe that the behavior of hydrogen is ideal and that of a single phase with the galactic arms immaterial or just a figment of our imagination. (This leads to the need to bring stars in to explain the galaxy, and the chicken/egg dilemma).
The Vegas odds at explaining away the winding problem is currently lie in favour of the “Density Wave Theory” that is quite arm wavy about traffic jams (in a rarefied gas?) and relies on the interference between stars and the hydrogen gas. While it is very easy to debunk this theory (ie. what happens before there are many stars? and what happens when the star to gas ratio changes?), at least the theory recognizes that the hydrogen must exist in two separate states or phases in order to have a chance at solving the winding problem. The theory assumes ISM and the stars themselves for the two phase/states of hydrogen mass that exist and that higher regions of ISM form as a result of highway traffic or some such thing. As it turns out, the theory goes very wrong right at the beginning of its formulation though in because it requires that stars orbit the galaxy at a different speed than the ISM. While this is indeed true, no explanation is provided as to why it is true.
Without an understanding of thermodynamics, the phase state of molecular cloud is not recognized, but merely considered a denser region of ISM. Here is a quote from the Wikipedia page on the density wave theory.
Originally, astronomers had the idea that the arms of a spiral galaxy were material. However, if this were the case, then the arms would become more and more tightly wound, since the matter nearer to the center of the galaxy rotates faster than the matter at the edge of the galaxy.[6] The arms would become indistinguishable from the rest of the galaxy after only a few orbits. This is called the winding problem.[7]
Aside from the first sentence, this entire quote is wrong. The authors incorrectly assume that the spiral arms are not material and are just regions of higher density – and this mistake forces them to use stars as a second state. What we have discussed in Part 3, and that I am going to elaborate on here, is that while it is true that the spiral arms indeed are regions of higher density, they are actually quite material – and represent a different phase or state entirely from the ISM between the spiral arms, with a different properties too as a result of basic fluid mechanics and thermodynamics. Even though both the spiral arms (MC) and the material between the arms (ISM) are made of hydrogen, they are very different – just like water vapour and raindrops are both made of water, but exist in very different states from one another. The realization that hydrogen can exist as two phases, frees us from the mathematical impossibility of constant orbital period with a single phase. It also releases us from the need to use either stars (or even “dark matter”) to explain spiral arms. What is does require though, is an explanation of why they don’t wind.
Give another play of Animation 1 above and I want to explain two end results from the winding process, but referring to our third force that was explained in Part 3 – viscous forces. One of things that could happen is when the angular momentum of the spiral arms are small (a low Reynolds number, laminar flow, scenario). The spiral arms closest to the black hole will orbit with a much shorter period (they will go around the black hole in much less time) in order to match centrifugal forces. Viscous forces will act to slow the particles down via friction against the slower orbiting spiral arms further out, which in turn will slow down particles yet even further out. As the spiral arms closest to the black hole continue to get slowed down they will continually get closer and closer to the black hole until it meets contact (with the even horizon, I suppose), where it will get sucked into the black hole. Eventually either the entire galactic material could get eaten. (Note that this process is similar to the accumulation of hydrogen on a protostar to form an actual star – but that is a for another post). Associated with the dissipation of kinetic energy due to viscous forces would be the heating up of the galaxy as a whole. This heating will reduce the viscosity of the hydrogen, but still the temperature – particularly close to the black hole would soar. We observe huge temperatures in the accretion discs of material in fairly close orbit to black holes. (At least here, we have the admission by necessity that frictional forces, or viscose forces actually exist).
The second thing that could happen is that the gravitational force of the black hole could be insufficient to contain the centrifugal force (angular momentum). In this case, the outermost galactic spiral arms will pull those closer to the centre faster and faster. As the arms move faster, until centrifugal forces will pull them away from the galactic centre and they become dispersed into space and lost to the galaxy. You may call this second thing the “unwinding problem”. (In fact, there are lots of examples where “unwinding” does take place, the most common observable situation is where the gravity of a different galaxy exerts a tidal force causing the galactic arms to unwind to some degree, only to rewind and join a new “pirate galaxy”. For now, however, we will assume that our galaxy that we are about to construct, with material spiral arms will be left alone.)
So we have to construct our galaxy with a number of constraints. Firstly, the flow must be turbulent with sufficient angular momentum that the Reynolds number is high. This is necesesary for our two phases of hydrogen to coexist in a dynamic manner. Secondly, regardless of radius, the gravitational force must equal the centrifugal force everywhere on the spiral arms or they will either fall into the centre or fly off. Thirdly, the centrifugal force, which is dependent on both velocity and radius of orbit, must result in the same orbital period everywhere on the spiral arms. While we showed that this is not achievable with hydrogen as a single phase, we will show how this is achieved with hydrogen existing as two phases – as a molecular cloud with its own gravity and as monatomic ISM that is so rarefied, that its gravity is almost immaterial. We will show how viscous forces, acting at a the high Reynolds number creates these two phases representing the spiral arms and the space between them, and how the galaxy configures itself in this spiral pattern.
In the case of spiral arms in a galaxy with a highly turbulent Reynolds number, the closing in of spiral arms caused by the winding issue will result in chaotic behavior due to viscous forces. Most of the turbulence is created in the ISM that separates and contains the relatively tranquil, higher viscosity MC phase at higher pressure and density. The pressure in the MC must be be sustained high enough to keep the majority of the total hydrogen mass in the diatomic molecular (H2) condition. Note that the arms cannot be merely composed of regions of higher pressure because under that scenario, there would be no difference between the viscosity of the spiral arms (MC) or the gaps (ISM), and we would be back to the winding problem – with no difference in the turbulence between the two. Instead, the arms must be material objects – different phases or manifestations of the same ingredients. This allows us to treat the spiral arms and ISM as distinct objects within the galaxy. This does not mean that the structure is static, however, the same ingredient – ie hydrogen – can be and is continually transitioning from one phase to another.
The short answer to the winding problem, is that the turbulence in the ISM, that occupies over 98% of the galactic volume, keeps the much more viscous, and dense, largely non-turbulent molecular clouds, that make up over 98% of the galactic mass, confined to spiral arms held apart by this turbulence. We could leave it at that, but a closer analysis of how this works will bear much fruit – including both the solution to the winding problem and also to questions about the relative movement of stars and dust to the spiral arms.
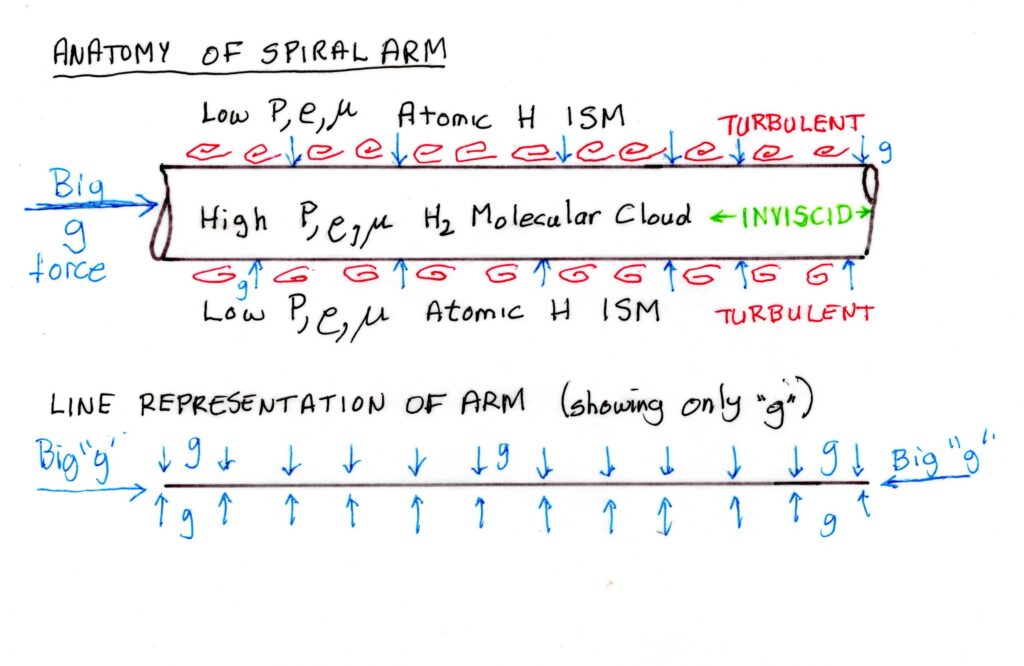
The spiral arms of H2 molecular cloud are the fundamental building blocks of our two phase galaxy. The arms are formed by turbulence within a second thermodynamic phase/state of monatomic hydrogen (ISM) surrounding and supporting the spiral arms. Bernoulli pressure, combined with the MC self-gravity, created by the denser molecular cloud also serves to contain them against their own internal pressure. The system is very dynamic, with molecules likely forming and pulled apart continuously at the interface. Erosion and deposition of material is likely also taking place at the interface.
In many diagrams we will be using a line representation, dropping the spiral arms width and eddies for ease of drawing.
Making up the vast majority of the galactic mass, it is the forces, or rather the balance of forces at play on the MC spiral arms that we will focus on. The MC arms are what really form the skeleton of the galaxy. The atomic hydrogen ISM, having very little mass, and very little viscosity has little influence on the main inertial forces at play. For now, we can consider the ISM of playing the sole role of helping to confine the molecular hydrogen to the arms through its turbulence and otherwise we don’t care too much about it. Only once we have built the skeleton of the galaxy using the arms, do we need to consider the circulation and dynamic behavior of the ISM – so that is for an entirely different posting.
What we will be focusing on is ultimately a free-body description of the MC arms, since this makes up (together with its star children) the overwhelming largest portion of the galactic mass. The MC material actually form long cylinders (or arms), whose properties need to be described to understand how they work. This understanding of the properties will pay dividends, not only forunderstanding the galactic structure and the winding problem, but also later in how dust and stars – the things we see and image – move about.
For the moment, imagine that our MC spiral arms are contained within a flexible plastic pipe, such as a garden hose, with the MC taking the role of water in the hose. When the contents of the hose are put under pressure, the hose will want to extend in a straight line, to balance the pressure forces on the outside of the hose and water will want to squirt out the ends. In our case, there is no plastic pipe to hold the pressure of the MC – and instead, it is the turbulent ISM that is playing this primary role. The ISM turbulence is continually moving past the MC at a much faster speed, causing the “Bernoulli” effect (Bernoulli’s principle) to occur in the molecular cloud. The pressure in the MC is held at a much higher than the moving ISM – so much so that the difference in both density and indeed molecular phase/state difference (molecular H2 vs atomic H) can be maintained between the ISM and MC arms. Once the MC are established via the Bernoulli effect, the arms are further confined by their own gravity. Much as it is hard to believe that one lighter gas can hold back and confine a more dense gas – it can when we incorporate viscous forces. As proof, I offer up the airplane that is held aloft by the fast moving air moving over the tops of the wings by the Bernoulli effect. (an airplane wing is more complex than this, so I don’t want to hear any objections about aeronautics).
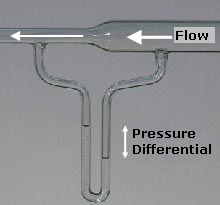
Formation of the galactic arms is likely initiated by the Bernoulli effect or principle, that a rapidly moving fluid exhibits a lower pressure than a slower moving one. In a similar manner, the fast moving ISM eddies can support a much high pressure within the relatively slow moving and tranquil molecular clouds.
credit: Wikipedia
In effect, the fast moving ISM actually forms the “garden hose” rubber, keeping the higher pressure MC confined and avoiding dispersion into the ISM. In many of its actions and reactions to forces, we will be treating it as such, and I have actually used a garden hose full of water as a thinking prop in the creation of this posting. Our arms of MC do differ from my garden hose example in few regards, the most important of which arises from scale. Our molecular cloud is big and it has considerable mass – so much so that it creates its own considerable gravity. On the galactic scale, this means that it pulls on itself both radially inward along the arm, conspiring with the ISM turbulence to keep the MC arm under pressure and confined.
Like a hose under pressure, our cylindrical molecular clouds will tend to form a straight line, surrounded radially by turbulent ISM, but open on the ends. Along the length of the cylinder, gravity pulls radially inwards, and over the length of the cylinder, there is no net forces. At the very ends of the arms, the inward forces on either end of the cylinder also directly oppose one another when the arm is straight, cancelling each other out just as the net forces cancel each other out radially. The net result is that there are no net forces on a straight MC arm, as the line representation shows. One thing to note is that at the arm ends, the longitudinal gravitational force also forces inward but with more strength than the radially force due to the arm geometry. Since this presents a radial versus longitudinal force imbalance on the arms, we will have to address this when constructing our galactic skeleton, by somehow “capping” or at least tapering the arms’ ends.
The confinement of the MC by the turbulent ISM also differ from water in a garden hose in another of aspect. If we want to move any of the water through a hose, we would require a pressure gradient, or force imbalance via the use of a pump or difference in height (head) to cause the water to move. This is because, water molecules in a hose will grip onto the inner edge of the hose that contains the fluid, under something we call the “no-slip” condition. In order to move fluid along the hose. molecules further in must move past these no-slip molecules creating viscous forces and energy dissipation to keep in order to keep flowing. When we water our gardens, we use the pressure in our pipe mains to push the water against viscous shear forces to get it to flow out the other end, where it has much lower pressure. (As an aside, an ideal gas is not subject to no-slip, and therefore exhibits no viscosity – despite what you might hear elsewhere).
The nature of the confinement of the MC by the ISM (and gravity) is that there is no actual hose, so we can shed the no-slip condition. The ISM outside the hose is moving very fast in its turbulence with respect to the MC cylinder. This turbulence actually invades the MC on the outside of the hose to form an extremely slippery boundary layer between the two phase that allows the contents of the cylinder to move lengthways along the cylinder without effort. The ability to move without drag or energy dissipation is what engineers call inviscid behavior (ie. without viscous forces) due the slippery boundary layer. For our galaxy this means the flow can occur along the spiral arms or even within the spiral arms with almost no effort or force required. Other examples of inviscid fluids are what are known as super fluids or indeed, the fictional “ideal gas” that is erroneously assumed. What this means for us is that we will have to exactly balance the forces along the length of our spiral arms for the galaxy to appear static, At the same time – any perturbations in part of the MC spirals or cylinders can be heals via flow from or to elsewhere.
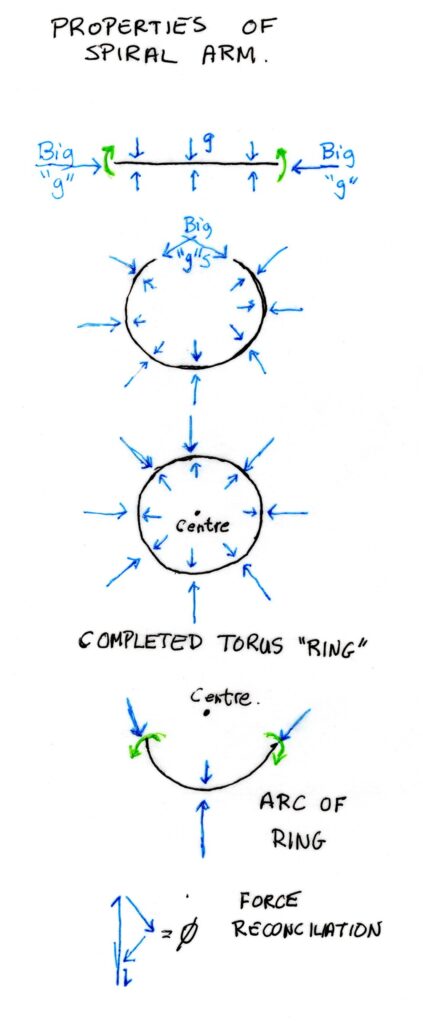
You may have already discerned that the arms in our galaxy are not straight, but are curved into a spiral – they don’t stick straight out from the centre. When subject to a bending moment, the arms will bend, creating gravitational forces that differ from straight arms. We can take our initially straight arm, and apply a bending moment at each of its ends, bending it around to form a ring. As we bend arm to complete a circle or ring, the once opposing ends of the arm would find themselves attracted to one another longitudinally, and when attached to one another will cancel each others longitudinal forces. The end result will be a ring of MC – forming a torus shape, just like the galaxy as a whole but much skinnier.
Just like a torus gravitational force described above and in Part 3, the outward gravitational force on the inside of the ring will be much less than the inward force on the outside of the ring will be. We will revisit this later in the post as it is very relevant to understand the overall gravitational field within the galaxy, but for now it is sufficient to understand that this creates an net inward force on the ring directly towards the centre of the ring. Left by itself, this would cause the ring to collapse to the centre. To avoid this happening to our ring,, we need to turn the ring about its centre to create an equivalent centrifugal force outward to stabilize it. The ring will adjust its size, by adjusting its radius of curvature until the gravity centrifugal force matches the gravitational force towards the centre. Note that this is a gravitation force, both on the ring, and created by the ring itself. The ring acts as if there was a mass at the centre, but there is none – the centre acts like a virtual mass to the ring around which the ring revolves.
What we are interested in is just a segments of our ring or an “arc” to use as a building block of our galaxy. Looking at arc, we see we have broken the end of the arc from the rest of the ring. As we will see, the spiral will be made up of such MC arm segments or MC arcs, with a varying radius of curvature, and having a varying virtual centre around which it will orbit. In building our galaxy from these arcs, we will be re-attaching them to one another, but there are a couple of things to note about the arc. Firstly, longitudinal gravity at the ends of the arc hold it in place with their inward force, but they no longer directly oppose one other. When we add the vectors of these forces together, the net result is a force that directly opposes but is equal in magnitude to the self-generating gravity towards its centre. In this way, the end forces on the arc can hold the arc in place by cancelling out the inward force due to gravity. However, there remains on our arc of the ring, a bending moment on the arc that wants to straighten it out again. This is because the net inward force of gravity on the ring is applied along its length, while the longitudinal forces (the Big “g”s appy at the ends). It is this straightening moment that we will use to counteract the “winding” moment we began with.
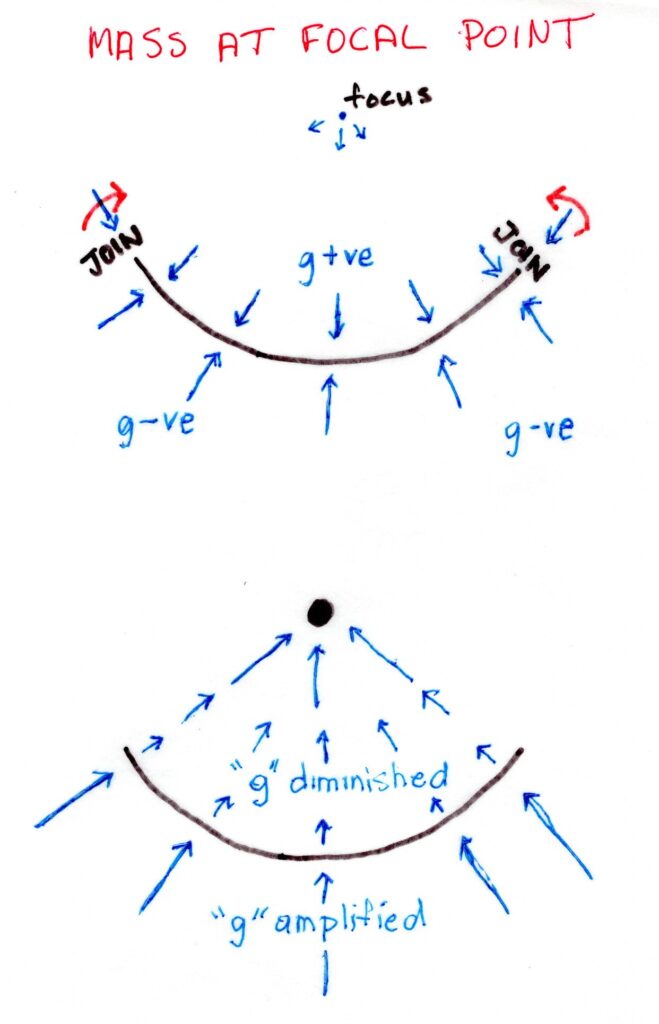
As in our naturalist/squirrel/tree fable, the role of tree will be played by the black hole at the true centre of the galaxy, the squirrel(s) are played by the virtual centres of the MC arcs, and the role of the humans will be played the MC arcs / arm segments themselves. One important point here, is that there really is nothing at the geometric centre, or focus of the arc, it is just that gravity on the arc is behaving as if there were. This is what I have been describing as “self gravity” – it is the geometry of the arc itself that causes the gravitational pull to the geometric centre (or focal point). It is very important that one understands this concept of self gravity of an arc. The gravity induced on the convex side toward the focus of an arc will be greater than the outward force, away from the focus point, on the concave side – just like the gravitational force on a torus. As far as the arc is concerned, there is a net gravitational force pulling it toward the focus, as if there was a mass at the centre.
Of course, we can put a mass at the focal point, and if it is sufficiently massive it will cause the outward force on the concave side to pull the opposite direction – by superposition of the two sources of gravity, the added mass and the arc itself. The gravitational force pulling the arc toward the centre will be stronger, being the sum of the two components. It is what is happening around the arc that will become very important when we want to describe the entire gravity field of the galaxy – both on the arc themselves in addition to space (ISM) between them. As the figure suggests, it is as if the magnitude of the gravitational pull toward the focal point is diminished on the concave side of the arc (less than it would be without the arc), while it is amplified on the convex side. It is helpful if we bear in mind that the arc itself acts like a gravity diminisher on the concave side, while an amplifier on the convex side.
An interesting thing happens when we place our mass, not at the focal point but offsetting it. Once again we have to superpose the gravitational fields of both the arc itself and our now offset mass. The gravity of the arc itself still points to its focus, but the superposition of both the fields created by both the arc and the mass cause the net force on the arc to seem if it is actually originating from a point in between the mass and the focal point. The precise point between the two depends upon the relative gravitational strength (caused by the relative amount of material) of the arc and the point mass. Between the arc and the mass, it is as if the overall gravitational field bends towards the mass in a curve as we move away from the arc.
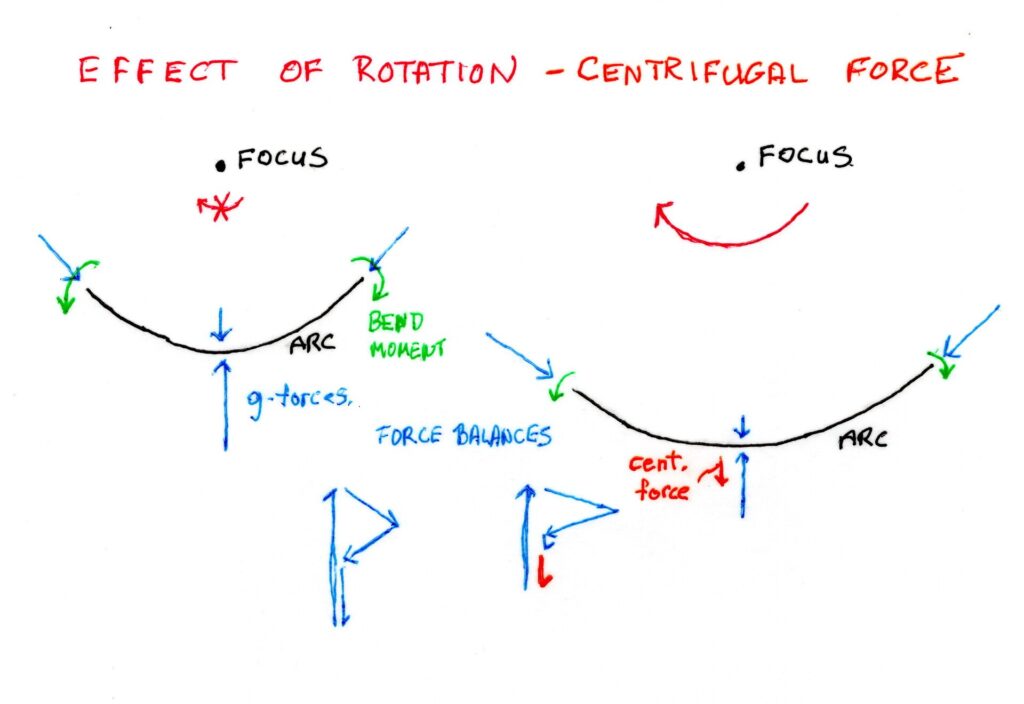
We are almost there…just one more diagram and force to consider, and that is our centrifugal force. If we started the arc spinning around its focal point (we have taken away the mass for the moment) it will experience a new apparent centrifugal force, in the opposite direction to net gravitation force on the arc. This will open the arc up, in terms of increasing its radius of curvature around the focal point relative to the stationary arc. In other words, the arc will straighten out somewhat, which will effect the degree to which end forces can offset the arcs gravity to the centre. The orbit will continue to be around the focal point because that is the arcs centre of gravity (but not its centre of mass) as well as the apparent origin of the directly opposing centrifugal force. Conservation of angular momentum dictates that as the arc expands, its period of rotation will slow, reducing the centrifugal force. The whole system will find a radius of curvature that, at equilibrates all of the forces involved. Another way to look at it, is that the arc will alter its radius of curvature about the focal point until all of the forces balance.
The final step is to construct our spiral galaxy with spiral arcs and a central black hole. This will involve combining what we know about the gravity of the arc with a point mass that does correspond to its focal point, and the orbit of the arc around its (now offset) centre of gravity. As in our naturalist/squirrel/tree fable, the role of tree will be played by the black hole at the true centre of the entire galaxy, the squirrel(s) are played by the focal centres of the MC arcs, and the role of the naturalists will be played by the MC arcs/arm segments themselves. At each point in in the spiral arm configuration, there are three forces that will play a role in our “free body diagram”:
- 1) The gravitation pull of the central attractor towards the true galactic centre (the tree). Note that this pull of gravity is not just due to the black hole, but result of the central attractor as well as the rest of the galaxy itself that is closer to the centre than the spiral arm segment under consideration, tempered by the outward pull of the galaxy that exists at a greater radius than the spiral arm segment. That’s a lot, I know, but just think of it as a black hole that generally increases in gravitational pull the further we move out in radius from it.
- 2) The “inward” gravitational pull of the spiral arm segment itself, that is directed to its geometric (virtual focal) centre, or focal point (the squirrel). Note that the focal centre is not at the same place as the galactic centre of mass, but the nonetheless, the arc segment is held in place by the end forces.
- 3) The outward centrifugal pull due to rotation. This pull will seem to original from the “centre of gravity” – a gravity weighted average point lying between the centre of the the galaxy and the segments own virtual focus point.
We will attempt to shown that these three forces are in balance from a reference frame that revolves at the same constant period, tau, as the galaxy itself. Since these forces balance in this reference frame at places along the spiral arms, we will see that the arms will not move relative to one another as the galaxy turns. The forces are reconciled by placing the force vectors end to end. If the result of vectors (arrows) are such that we end up on the starting place, so that there are not net forces this will cause the body to move in our rotating frame of reference. We will see how the spiral arms react to any perturbations to this pseudo-steady state condition to restore balance in the forces. In other words, if you jostle the galaxy, it will restore balance rather than be unstable. Since each of these forces are balanced, everywhere along the spiral arms, then the arms can rotate, like the hand of a stopwatch, as if they were solid, and the winding problem will be solved. We now have all of our ingredients and know all of our forces, so let’s finally get started.
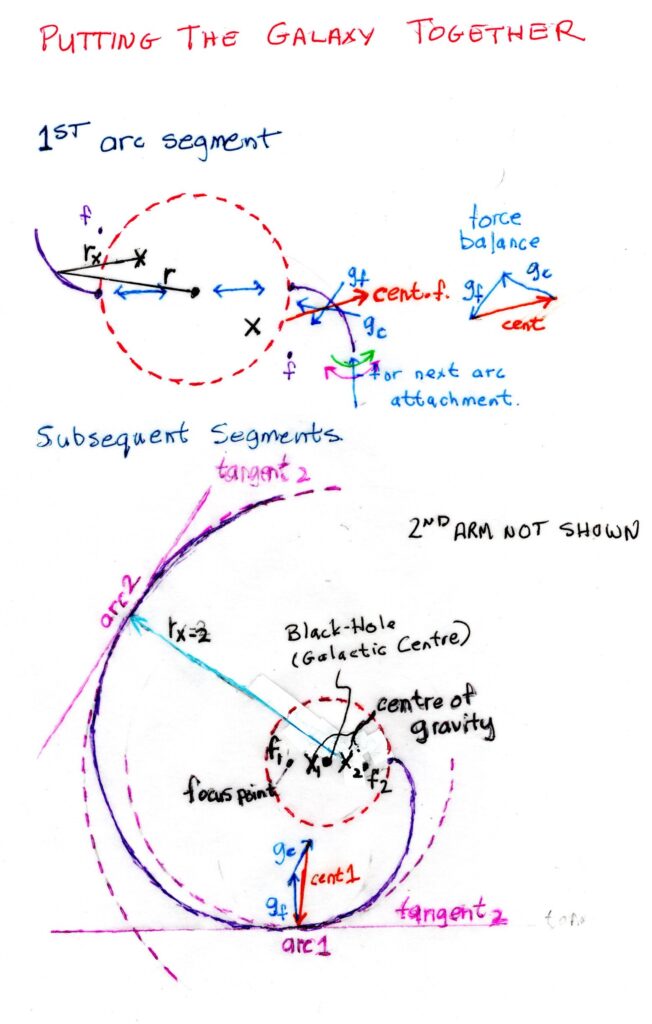
We will be building our galaxy with two continuous spiral arms (the most common of spiral galaxies), but the principles of more arms will work just as well. We have described the inner edge of the galactic torus (donut hole of our galaxy) as the radius where the net gravitational force within the galaxy is lowest. At this point, anywhere around the centre, we will start our first spiral arm. We will point our first arm, end on, with its high gravitational end pointed directly at the black hole / central attractor. At this point the first segment of the spiral arm will want to point directly outward. As soon as we attach this arm, the gravity of the black hole centre will align with the mass of the first arm to create a gravitational maximum on the opposite side of the galaxy. We will attach the second arm at this opposite side (180 degrees or pi radians) of the black hole. If both arms are approximately equal, this will leave the galaxy balanced with its true centre of gravity at the black hole. (This is why most galaxies have two spiral arms, but more arms are permitted to achieve the same thing.) The trick is, that as long as whatever we do the manipulate the gravity and other forces on one spiral arms, as long as (at least approximately) the same thing is done with the other spiral arm, the true centre of gravity of the entire galaxy will remain at the central attractor – the tree in our fable. This simplifies our analysis and allows for the centre of gravity of our MC arc segments to differ from the galactic centre of gravity without upsetting the apple cart – as long as the same is repeated on the opposite side of the galaxy. We also can restrict most of our analysis to one spiral arm, noting that the results will also apply to the other one.
As we add length to our first spiral arm attachment point, gravitational pull of the galaxy (Force 1 – gravity pull of the galaxy) will not be able to keep up with centrifugal forces causing the “loose end” of the first spiral arm to lag in orbit. This lag will create and a bending moment will be imposed on the first segment of the galactic arm (this is indeed the winding problem). This bending moment will force the segment to become concave opposite to the direction of galactic rotation and form an arc. For our case, we will assume the galaxy is turning counterclockwise, such that the bending will be convex to the left and inward. This is where the cool stuff happens.
As the segment becomes bent, it creates its own gravitational force (Force 2 – gravity pull of the arc segment, labelled gf) pointed directly towards its focal point, just like the arm segment in the ring. This is a virtual point, and has no real mass, but as far as the segment is concerned, it attracts the middle of the segment / arc as if there were a mass there. This focal point or centre of gravity does not coincide with the black hole at the centre of the galaxy – just like our offsetting mass case – and the pull of centre of the galaxy is labelled “gc“. It is as if there are two masses pulling on our arc, a real one located at the galactic centre and a virtual one, located at its centre of curvature or focus – taking the roles of the squirrel and the tree. To determine to overall gravitational pull on the arc, we can graphically add two arrows (with magnitude and direction) corresponding to the pull of gravity from these two forces. Adding these arrows together point to the arcs centre of gravity, lying between the focus and the black hole depending on the the relative strength of the two gravity vectors.
When we construct this diagram, we find that the net gravitational pull is coming from a place that lies on a straight line between between the centre of the galaxy (black hole) and the centre of curvature of the arc. This point is, in reality, the solution to an ordinary differential equation describing the whole gravitational force, but in order to stay away from calculus, it is basically a weighted average based on the two gravity force acting on the arc. Determining this point creates the true centre of gravity as experienced by the arc. If our naturalist was in orbit around our tree and squirrel, it would be the equivalent of the centre of mass between the tree and the squirrel. Again, the point can roughly be determined graphically by drawing a line between the galactic centre and the centre of the radius of curvature of the arc.
Just as our naturalist revolves around both the tree and squirrel, our arc segment actually revolves around this new overall centre of gravity that we have determined with a period still equal to tau. This centre of gravity, in turn, revolves around the centre of the galaxy with a period, again equal to tau. In a rotating frame of reference, the arc, its virtual centre of gravity and the centre of the universe are not moving relative to one another. The virtual centre of gravity has no mass, so there are no forces on it, but there is one more force to address on the arc itself, and that is centrifugal force. Since the arc is rotating about its virtual centre of gravity, this point also serves as the origin for the centrifugal force. For the arc to remain stationary,in our rotating frame of reference this centrifugal force must exactly match the magnitude of the net gravitational force towards its centre of mass so that they cancel.
This matching of centrifugal force of the arc with its gravitational pull does not happen by coincidence. It is done by the arc itself through the use of two independent variable it has at its disposal. The first variable is the radius of curvature of the arc. This controls the stretch of the strength of the gravitational force and alters the position of the arcs focal point. If the total gravitational force on the arc is less than the centrifugal force, it will bend the arc more, so that the total gravity force increases to counter it and visa versa. The second variable the arc has is to vary the density of the arc itself. This can be done via amassing mass from further out of the spiral arm, or by sending mass further afield. Recall, that flow along the spiral arm is inviscid. Together with the radius of curvature, the centre of gravity of the arc can be varied until both all forces match. In addition, the manipulation of these variable allows the galaxy to remain stable under mild to modest perturbations. Such variations can include the creation of stars, the variability of turbulence, the overall galactic circulation system, and finally, even perturbation that occur on the opposite spiral arm. Most of these will be covered in Part 5.
There is one last thing we need to address on our first arc section and that is the far end of the arc section which we kind of left dangling. This, of course, forms the fixing point for the next section of arc that we will be attaching. The position of the attachment is fixed in rotating space, just as the first end of the arc. Wherever we make this attachment point will cause a bending moment due both ends being fixed, while the gravitational pull of the arc, acting towards its focal point, attempts to straighten out the arc. This bending moment is in the opposite rotation to the winding moment that prompted this discussion in the first place.
The remainder of the construction of the spiral galaxy simply consists of adding more arc segments to the free end, created an expanding spiral pattern outward until we eventually end out of galaxy. I have shown two additional point on the figure above, one where the forces are balanced, and another showing how the radius of curvature, the focal point, and the centre of gravity are determined. At each point along the spiral arms, the forces on each arc cancel out. As we move outward from the centre, the focus point of the arc moves further away from the arc as the radius of curvature gets larger. Towards the outside of the galaxy, it will move from being closer to the arc than the galactic centre, to farther away when the arc itself is orbiting in a radius that is larger than the the radius from the galactic centre. All along the way, a similar construction is occuring with the second spiral arm, resulting in centre of gravities or arc segments that are 180 degrees from the first spiral – leaving the complete centre of gravity of the entire spiral at the black hole. (Note that only one of the spirals is shown in the diagram).
Overall the galaxy is using a few tricks, not available to a single phase representation, to keep all the arms rotating at the same period – like the hand of a stopwatch. The first trick is the use of arcs that complement the gravitational pull of the black hole such that the net gravity gets larger with radius from the centre. The second is to change the direction the arc is facing so that the centrifugal “radius” component of the radial force is adjusted to that the gravity force matches it. This is done by altering the radius of curvature of the arcs, and the distribution of material along the arc – from close to the black hole, all the way to the outer reaches of the galaxy.
In reality, the spiral galaxy will not be composed of discrete segments as we have described, but rather a continuous spiral curve with a continuous transition of the radius of curvature, and a continuous change in the spiral arm density as well. We can take the force analysis described here, and apply it to our face on images of galaxies as well. The technique consists of drawing a circle to match the radius of curvature at any point on one of the spirals. Since the spiral gets tighter towards the galactic centre and looser away, you will have to find a compromise on the side where the tangent of the circle matched that of the spiral arm. The centre of the circle forms the focus of the spiral arc. Then you can draw a line between this focus point and the black hole at the whole galactic centre, and estimate where the centre of gravity is for that point on the arc. I put the image into powerpoint to do this fun analysis.
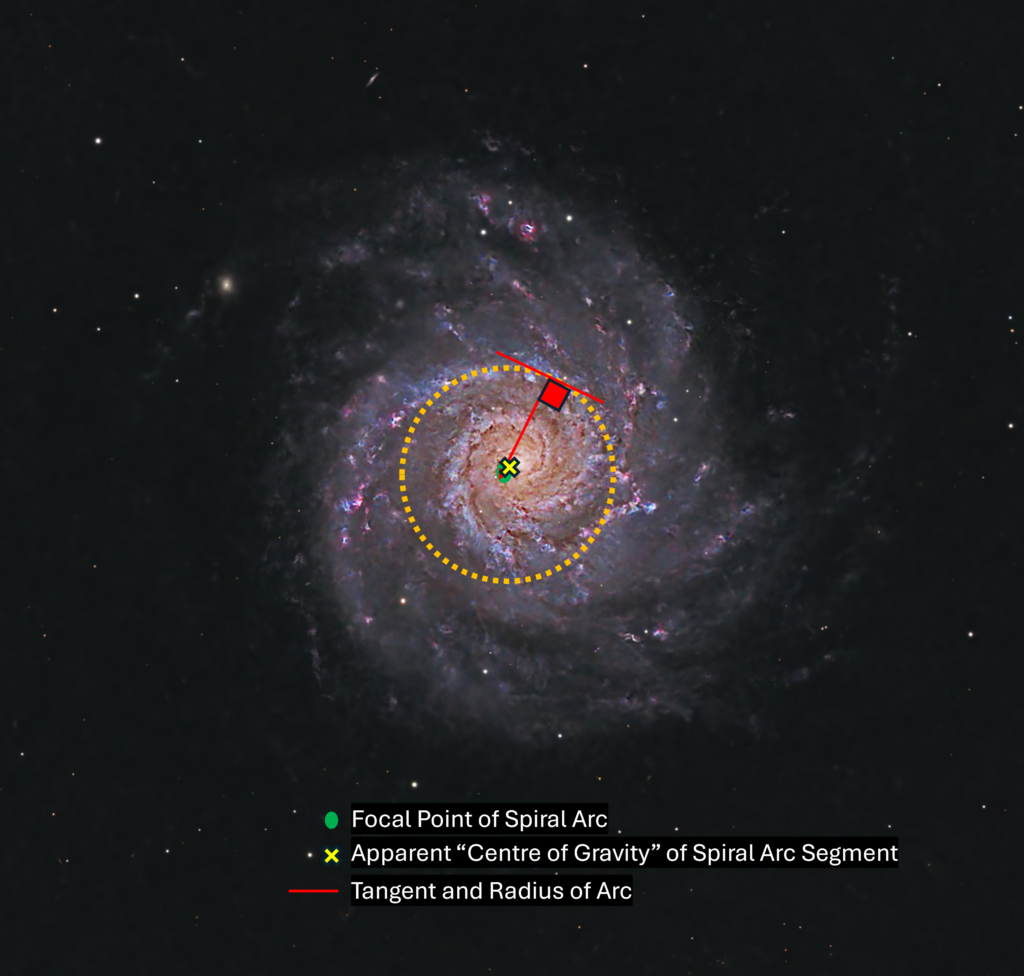
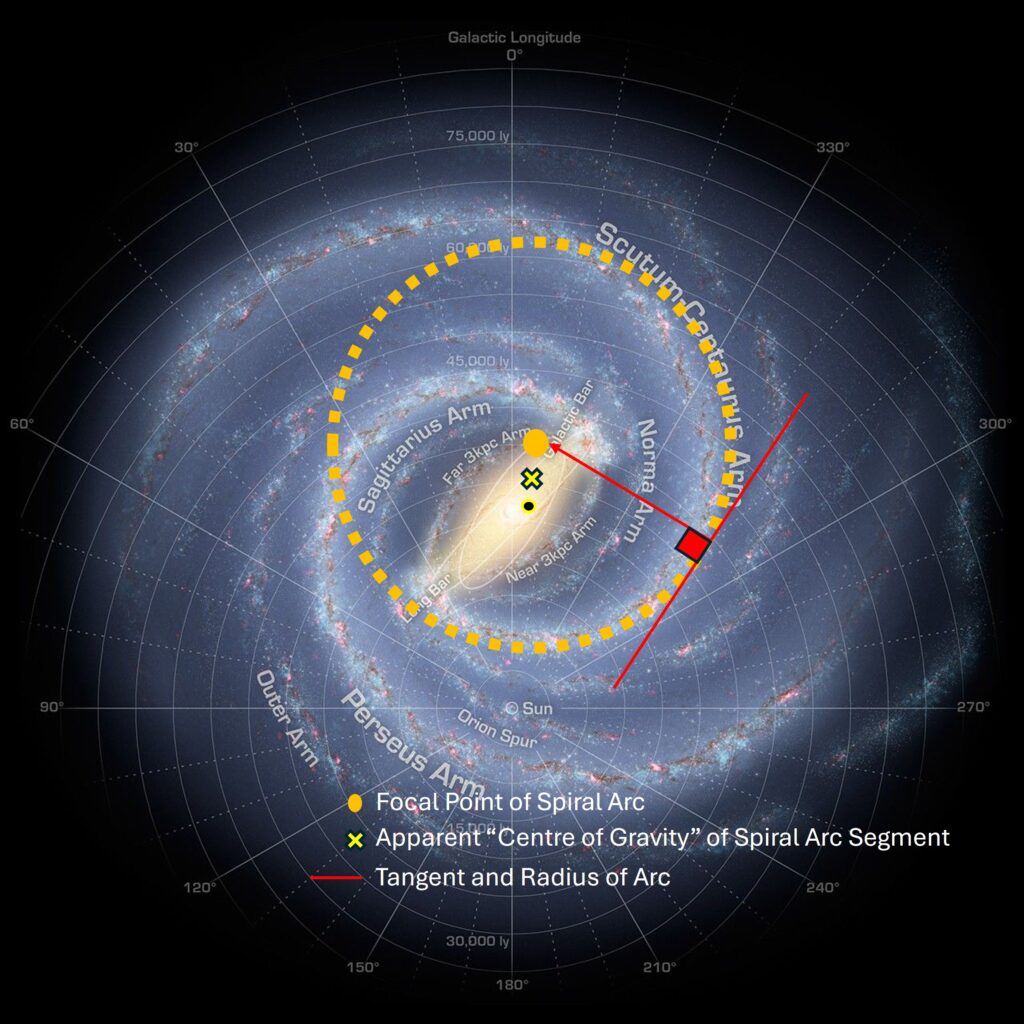
So that is the winding problem, well and truly solved. However, while we are at it, it will be useful to show how the spiral arms effect the gravitational field of the galaxy as a whole – not only at the arcs, but between them as well. This will be tremendously useful, when we go on to demonstrate that there is no dark matter required to make the star orbit velocities make sense. Once we do that, we can show that via an astrophysical accounting error, there is likely no dark matter required to make the orbits between galaxies work either. In fact, doing this extra bit of work, will end up showing, in Part 5, that there is no justification for the presense of dark matter at all!
So lets look at the gravitational force along an arbitrary radius through the galaxy. At first, we described this as potentially having a g-force as a linear function of radius in order to solve the winding problem. However, what we get is a periodic g-forces that does get stronger the further we move out. If we look at the places where g-force is strongest, this is where the galactic arms reside in our arbitrary cross section. These arms kind-of sort-of form a linearish pattern in our plot because we are using actual radius instead of their rotational radius, which can be smaller than the actual radius (for arm segments close to the centre) and larger on the outside of the of the galaxy.
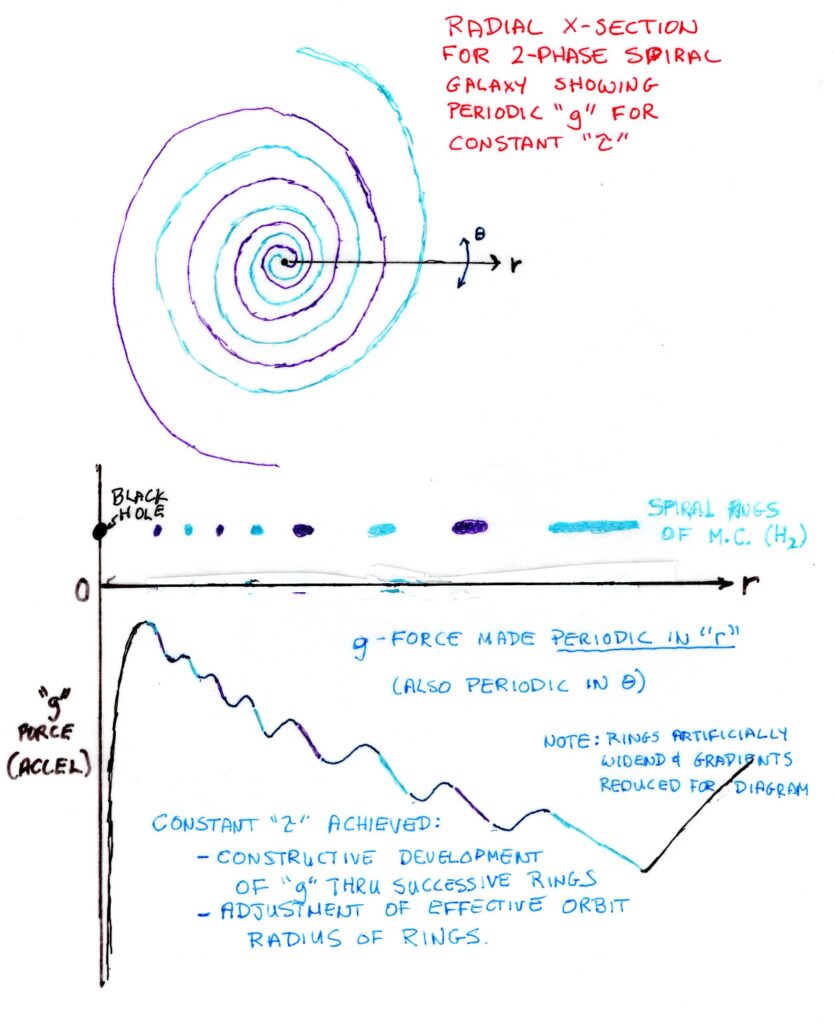
Between the galactic arms the g-force is anything but linear – once again forming a periodic functions. All I can really say about it is that the ISM between the galactic arms is likely having a field day here with its turbulence. Fortunately, the ISM, while taking up a lot of the space, actually represents very little of the galactic mass and has an extremely low viscosity – so we don’t really care if it is having a turbulent field day between the galactic arms. Since the viscosity is so low, the total dissipation of energy to heat is very low. At the same time, this turbulence is necessary in order to create the galactic arms in the first place. One final remark to be made, is that this cross-section is arbitrary and in any other cross section, the galactic arms will appear at different radii – the net result is that the gravitational field will be periodic in both polar directions – radially and in the angular direction. This will result in some interesting observations on star movement (once we add them) such that observers might be tricked into believing there is a magical thing called dark matter – but we will know better.
So we have come full circle on our analysis and know what the galactic spirals are, that they are indeed material, know how they move, and why they don’t spiral upon one another. Unfortunately, they remain largely invisible to us (with one exception that I will detail in the next post). The only thing left in this series will be to make the galaxy visible to us by first adding what I call jewelry – the stars, the dust, and the emission regions. In Part 5 I will discuss the strange movement of stars and the circulation system of the galaxy, why dust appears where it does, and what causes hydrogen emission regions associated with star birth. I will also show why, by counting only IR emission of hydrogen atoms, astrophysicists may have made and accounting errors in determining the true mass of H2 within the galaxy.
Part 5, will be my final long posting on this series on spiral galactic structure, and I will be getting back to my own focus of imaging. In the meantime, I am hoping you are finding this interesting and helpful. I do promise that you will never look at a squirrel in a tree the same way again.